0-Layer Normalization

Layer Normalization

层标准化 arXiv:1607.06450v1 2016年

背景

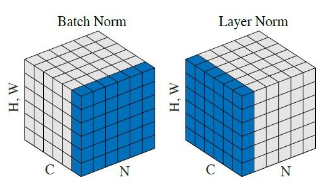
BN（2015）、LN做为常用的标准化方法，不同之处就是在于对于激活函数的改变方式。标准化的目的是为了把输入转化成均值为0,方差为1的数据。

BN通过在深度神经网络中加入额外的归一化阶段来减少训练时间，除了训练时间的改善外，批量统计的随机性还可在训练过程中充当正则化器。但是BN在处理RNN任务序列化数据不适用，并且BN依赖Batch Size,所以引出了本文，层归一化的思想：与批量归一化不同，所提出的方法直接从隐藏层内神经元的总输入中估计归一化统计数据，因此归一化不会在训练案例之间引入任何新的依赖关系。

实验方法

层规范化LN就是为了克服BN的缺点，通过固定每层内输入总和的均值和方差，可以减少“协变量偏移”的问题。在RNN中，例如输入文本处理任务，训练案例中的不同句子长度不同是很常见的，使用BN的话，需要为序列中每个时间步长计算和存储单独的统计数据，如果测试数据比训练数据长，那么就会出现问题，而LN的归一化项仅取决于当前时间步长对层的输入求和，并且只有一组共享的增益和偏差参数。

1.权重和数据变换的不变性

两个标量$\mu$和$\sigma$将总输入$a_i$归一化到神经元，之后为每一个神经元学习自适应偏差b和增益g。
$$
h_i=f(\frac{g_i}{\sigma_i}(a_i-\mu_i)+b_i)
$$
在经过权重与数据的重新缩放和重新居中后：
$$
h_i^丿=f(\frac{g_i}{\sigma^丿}w_i^Tx^丿-\mu^丿)+b_i)=f(\frac{g_i}{\delta\sigma}\delta w_i^Tx-\delta\mu)+b_i)=h_i
$$
重新缩放单个数据点不会改变模型在层下的预测归一化，类似于层归一化中权重矩阵的重新居中，可以表明批量标准化对于数据集的重新居中具有不变性。

2.学习过程中参数空间的几何形状

本部分，作者介绍了，通过权重向量的增长来隐性降低学习率和学习输入权重的大小的选取方法，归一化模型仅取决于预测误差的大小。标准化模型中传入权重对输入的缩放更具鲁棒性及其参数比标准模型更精确。详细推导见附录。

实验结果

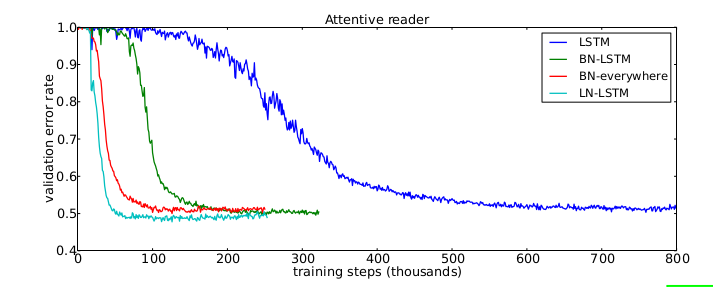
专注阅读模型的验证曲线，可以看出使用LN方法在最少的训练步骤获得了低错误率。

结论

Layer Normalization (LN) 的一个优势是不需要批训练，在单条数据内部就能归一化。LN不依赖于batch size和输入sequence的长度，因此可以用于batch size为1和RNN中。LN用于RNN效果比较明显，但是在CNN上，效果不如BN。