0-Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or −1
Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or −1

arXiv:1602.02830v2 [cs.LG] 29 Feb 2016
背景
本文提出了一种称为二值化神经网络(Binarized Neural Networks, BNNs)的方法。这种方法对神经网络中的权重和激活值进行二值化处理,将它们限制为+1或-1。这种处理方式的主要优势在于:计算效率:二值化操作可以大幅减少计算所需的复杂度,使得计算变得更为简单和快速。内存节省:由于权重和激活值仅需存储为1位(bit),内存需求显著降低。硬件友好:这种方法特别适用于在硬件上实现,如FPGA和ASIC等专用集成电路。
实验方法
二值化方法:
(1)Derterministic
$$
x^b=Sign(x)=\begin{cases}+1& if\ x\geq0\-1& \text{otherwise}\end{cases}
$$
(2)Stochastic(硬件生成随机数)
$$
x^b=\begin{cases}+1& 随机计算p=\sigma(x) \-1&1-p \end{cases}
$$
本文选用第一种方法,避免了使用硬件生成随机数。
二值化网络:
(1)二值化网络只是将网络的参数和激活值二值化,没有改变网络结构,且输出层的概率输出仍是浮点型,其前馈模型的公式表示为:
$$
x^k=\sigma(W^k·x^{k-1})\
x^k是第k层输入,W^k是第k层权值矩阵,\\sigma()为非线性激活函数。
$$
(2)二值化激活函数:
$$
\sigma(x)=sign(x)
$$
训练过程:
(1)前馈过程:先将实数型权值参数二值化得到二值型权值参数,即$W^b_k=sign(W_k)$。然后利用二值化后的参数计算得到实数型的中间向量,该向量再通过Batch Normalization操作,得到实数型的隐藏层激活向量。如果不是输出层的话,就将该向量二值化。
$$
x^k=\sigma(BN(W_b^k·x^{k-1}))=sign(BN(W_b^k·x^{k-1}))
$$
(2)反向更新:

作者为了解决sign的导数几乎处处为零的问题,对sign(x)进行了改写,让其在-1和1之间加一个线性变化的过程。
实验结果
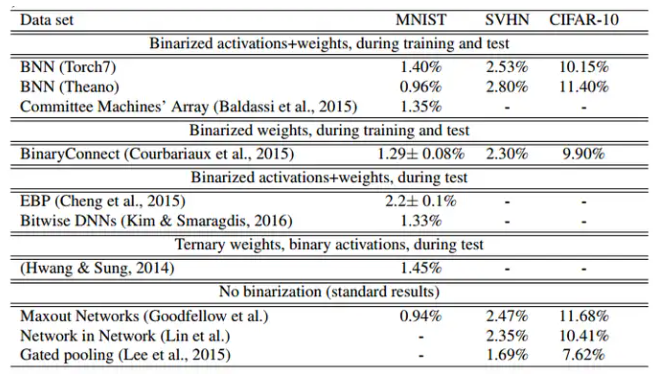
展示了在CIFAR-10和SVHN等多个数据集上的实验结果,表明二值化神经网络在保持较低计算和内存开销的情况下,依然能够取得接近甚至超过传统神经网络的性能。
与实值网络相比准确率并没有太多降低,时间复杂度却可以降低60%。相对于32bit的DNN,BNN内存需求量减少为原来的1/3
结论
二值化神经网络通过简化计算和降低内存需求,为神经网络的实际应用提供了一种有效的方法。特别是在计算资源有限的场景下(如移动设备和嵌入式系统),这种方法具有显著的优势。